[2] 딥러닝 이해하기

1. 딥러닝 원리 이해하기
2. 인공신경망의 신호 전달 원리
3. 인공신경망의 학습 원리
4. 텐서플로 플레이그라운드로 딥러닝 체험하기
5. 다양한 딥러닝 기술 살펴보기

딥러닝 원리 이해하기

딥러닝(Deep Learning)

• 사람의 뇌에서 이루어지는 원리를 이용하여 인공지능을 만드는 방식

인공신경망(Artificial Neural Network)

• 신경망을 사람들이 인공적으로 만든 것
• 인공신경망에서는 신경망의 최소 구성 단위인 뉴런이 다른 뉴런과 연결된 모습을 각각의 층, 즉 레이어라는 개념을 사용하여 연결하고 있음
• 인공신경망 모델은 입력 받은 데이터를 사용하여 추론한 결과를 보여줌
• 이때 신호를 정확한 출력값으로 보내는지 그렇지 않은지가 바로 그 인공신경망 모델의 성능을 결정함
• 이때 인공신경망 모델이 신호를 정확한 출력값으로 보내지 않는다면, 정확한 출력값으로 보낼 수 있도록 신호 세기를 조정하는 과정이 바로 인공신경망의 학습 과정임

입력층	은닉층	출력층	심층 신경망	딥러닝
데이터(x)를 입력받는 층	입력층에서 들어온 데이터가 여러 신호로 바뀌어서 출력층까지 전달됨	'이 출력층에 어떠한 값이 전달되었냐'에 따라 인공지능의 예측 값이 결정됨	Deep Neural Network, DNN	심층신경망이 학습하는 과정
	이때 연결된 여러 뉴런을 지날 때마다 신호 세기가 변경됨		레이어가 한 층으로 구성된 것이 아니라 깊은 층으로 구성된 인공신경망

인공신경망의 신호 전달 원리

• 신호를 받는 뉴런은 하나의 뉴런에서만 신호를 전달받는 것이 아니라, 여러 뉴런에서 신호를 전달받으며 인공신경망도 이와 비슷함
• 이때 단순하게 신호를 전달해 주는 것이 아니라 신호 세기를 변경해서 전달함
• 뒤쪽으로 전달되는 신호 세기는 앞쪽 뉴런에서 전달된 신호의 값에 가중치라는 값을 곱하고, 편향을 더해서 다음(뒤쪽)으로 전달함
• 가중치는 심층신경망의 각 뉴런과 뉴런을 연결하는 선에 있으며, 각 선에는 가중치라는 서로 다른 값들이 저장되어 있음
• 편향 값은 각 층에 하나의 값으로 존재함

인공신경망이 학습한다.
= 가중치와 편향 값을 데이터에 맞게끔 정교하게 맞추어 간다

활성화 함수

• 들어오는 신호 세기를 조절함
• 뉴런이 전달하는 신호는 가중치와 편향을 거침
• 서로 얽혀 있는 뉴런은 다음 뉴런에게 신호를 어떤 때에는 전달하고, 어떤 때에는 전달하지 않음
  • 특정한 전기적 신호가 어떤 값(역치) 이상 전달외었을 경우에는 다음 뉴런으로 신호를 전달하지만, 어떤 값(역치)보다 작을 경우에는 전달하지 않음 
• y = f (z) , f: 활성화함수, z: w(i) * x(i) + b
• 여러 뉴런에서 들어온 신호 세기를 특정한 값으로 바꾸기 위해 활성화함수 사용
• 활성화 함수는 신호 세기를 조절하는데, 특히 레이어와 레이어 사이에 있어서 여러 뉴런에서 특정한 뉴런으로 들어가는 신호를 종합해서 하나의 값으로 바꿔주는 역할을 함

뉴런 -신호 1-> 

뉴런 -신호 2->          활성화 함수       -신호-> 뉴런

뉴런 -신호 3-> 

 

시그모이드 함수

• S자형 곡선 또는 시그모이드 곡선을 갖는 수학 함수

주로 S자형 곡선을 통칭한다

• 로지스틱 함수: 시그모이드 함수의 대표적인 예로, 여러 뉴런에서 들어온 신호 세기를 모아서 그 값이 0보다 클수록 1에 가까운 숫자로 바꿔주고, 반대로 신호세기가 0보다 작을수록 0에 가까운 숫자로 만들어주는 특징을 가진 활성화 함수

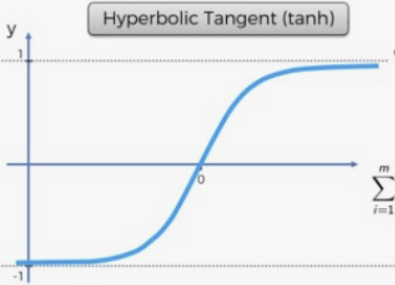
하이퍼볼릭 탄젠트 함수

• 값이 작은 신호를 -1에 가까운 숫자로 바꾸어서 내보냄
• 시그모이드(로지스틱)함수는 출력값이 0에 가까워지면 잘 학습하지 못한다는 단점이 있지만, 하이퍼볼릭 탄젠트 함수는 0이 아닌 -1 값을 출력하기 때문에 이 한계를 넘을 수 있음

렐루 (Rectified Linear Unit, ReLU) 함수

• 입력값 < 0 : 0
• 입력값 > 0 : 입력 받는 값

Leaky 렐루 함수

• 입력값이 음수일 경우에 출력값이 0으로 같다는 단점이 있어서, 이를 해결하기 위해 Leaky 렐루 함수가 새롭게 개발되어 사용되고 있음
• 전달받은 신호 세기의 합이 음수일 경우에 0인 값을 출력하지 않고, 미세하게 나마 차이가 나는 음수의 값을 전달함

소프트맥스 함수

• 최종 결괏값을 정규화하는데 사용하는 함수
• 인공신경망의 출력층에 소프트맥스 함수를 사용하면 분류 문제를 해결할 수 있음
• 소프트맥스 함수는 인공신경망 모델에서 항상 사용되는 것이 아니라 분류 문제에서 사용되는 함수라고 볼 수 있음

오차 줄이기

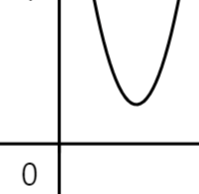
경사 하강법(Gradient Descent)

• 기울기로 가중치 값을 변경하는 경사 하강법
• 가중치에 따라 오차가 달라짐
• 기울기를 보고 기울기가 줄어드는 쪽으로 가중치 값을 이동

X축: 가중치, Y축: 오차

• 가중치에 따라 신호 세기가 바뀌고, 그에 따라 인공지능의 결괏값이 결정됨
• 인공지능의 학습 = 가중치와 편향을 적절하게 조절해가며 최적의 값을 찾는 과정
• 기울기가 가파를수록 다음 값의 변화가 크다는 것을 알 수 있고, 기울기가 완만할수록 값의 변화가 얼마 없다는 것을 알 수 있음
• 이러한 미분 개념을 사용하여 인공신경망의 오차를 수정해나감
• 경사 하강법의 핵심은 미분이며, 이를 정확하게 이해하려면 일정 수준 이상의 수학 지식이 필요

오차 역전파법 (Error Backpropagation)

인공신경망을 설계하면 가중치의 값이 한두개가 아니라는 문제가 있음

• 오차를 끝에서부터 거꾸로 가면서 줄임
• 마지막부터 처음까지 되돌아가면서 경사 하강법을 사용하여 각각의 가중치 값을 수정함
• 뒤로 가면서 수정한 다음 다시 한 번 데이터를 흘려보낸 후 결괏값을 살펴봄
• 그 결괏값이 정답값과 얼만큼의 차이가 있는지 살펴본 후, 다시 오차 역전파법을 사용하여 가중치를 수정함
• 이렇게 오차값을 계산하고, 그 오차값에 따라 가중치를 점점 수정해나가는 모습이 바로 [ 인공신경망에서의 인공지능 학습 방법 ] 임 

텐서플로 플레이그라운드

- Epoch: 전체 데이터를 사용하여 인공신경망이 학습한 횟수
- Learning rate: 오차값을 최소화하기 위해 각 뉴런을 연결하는 가중치 값을 수정해 나가는데, 한 번 수정할 때 얼마    만큼 수정할지를 결정
- Activation: 활성화 함수, 여기서는 ReLU, Tanh, Sigmoid, Linear 함수 사용 가능
- Regularization: 규제, 과적합을 줄이기 위함, 여기서는 L1규제와 L2규제 사용 가능
- Regularization rate: 규제의 강도
- Problem type: 여기서는 분류와 회귀로 나눔
- Output: 출력층
     - 파란색 점이 있는 곳과 주황색 점이 있는 곳이 2개 영역으로 구분됨
     - 그래프에서도 볼 수 있듯이 오차 또한 0에 가까워지고 있음
- Hidden layers: 은닉층
     - 신경망 층의 개수를 수정할 수 있음
- Data: 데이터의 입력 형태 선택
     - 기본적으로 X축과 Y축의 값을 입력
     - 데이터의 형태, 시험 데이터와 훈련 데이터의 비율 (Raio of training to test data), REGENERATE(재생성) 버튼         을 클릭
     - FEATURES에서 입력값을 수정해 보면서 어떤 입력값이 가장 좋은 모델을 만드는 데 사용될 수 있는지 살펴볼         수 있음
     - 또한 데이터의 모습과 비슷한 입력을 선택하니 금방 학습이 진행되는 것을 확인할 수 있음

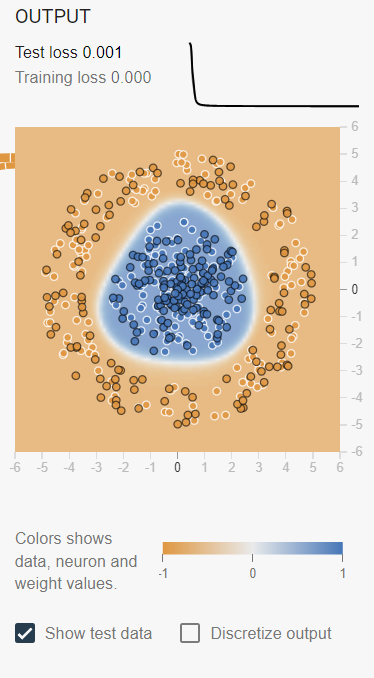
Show test data 버튼을 클릭하면 시험 데이터를 살펴볼 수 있는데, 데이터를 학습 데이터와 시험 데이터로 구분하지 않는 이유는 신경망을 훈련하는 데 모든 데이터를 쓰지 않고 일부분만을 사용하기 위해서임
Test loss: 시험 데이터를 신경망에 넣었을 때 오차값
Training loss: 훈련 데이터에 대한 오차값

다양한 딥러닝 기술

1. ANN(인공신경망, Artificial Neural Network)
2. DNN(심층신경망, Deep Neural Network)
3. CNN(합성곱신경망, Convolutional Neural Network)
4. RNN(순환신경망, Recurrent Neural Network)
5. 생성형 인공지능: 새로운 무엇인가를 만들어내는 기술
6. 딥페이크(Deepfake): 기존에 있던 영상이나 사진에 새로운 사람의 얼굴이나 특정 부위를 합성한 것